Funciones logarítmicas y exponenciales

Funciones logarítmicas y exponenciales
La función logarítmica "básica" es la función, y = log b x, donde b > 0 y b ≠ 1.
La gráfica de la función logarítmica y= log 10 x se muestra a continuación.
Resultado de imagen para Funciones exponenciales
Observe que la función logarítmica es la inversa de la función exponencial y = b x y tiene las siguientes propiedades.
1.    El dominio es el conjunto de todos los números reales positivos.

2.    El rango es el conjunto de todos los números reales.

(Ya que la función logarítmica es la inversa de la función exponencial, el dominio de la función logarítmica es el rango de la función exponencial y el rango de la función logarítmica es el dominio de la función exponencial)
3.    La función es continua y uno-a-uno.
4.    El eje de las y es la asíntota de la gráfica.
5.    La gráfica intersecta al eje de las x en (1, 0). Esto es, la intercepción en x es 1.








Función logarítmica natural
El logaritmo con base e es llamado el logaritmo natural. Se denota por ln x . La función logarítmica natural, y = ln x es la inversa de la función exponencial natural de base, y = e x .
La gráfica de la función logarítmica natural y = ln x se muestra a continuación.
Resultado de imagen para Función logarítmica natural


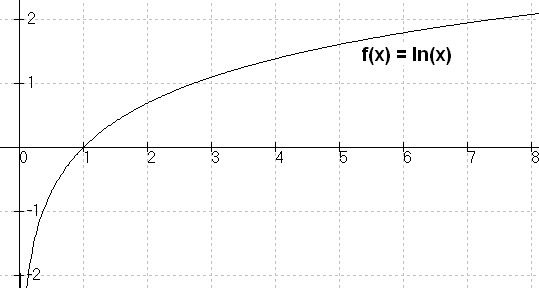
Funciones exponenciales
La función exponencial, es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828.; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita o bien como un límite de una sucesión.{\displaystyle e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\ldots }

Propiedades
La función exponencial (y exponenciales en base distinta a e) satisfacen las siguientes propiedades generales.
·         Son las únicas funciones que son igual a su derivada (multiplicada por una constante, en el caso de que tengan una base distinta a e)
·         exp (x + y) ­­­= exp (x) . exp (y)
·         exp (x – y) = exp (x) / exp (y)
·         exp (-x) = 1 / exp (r)
·         exp (0) = 1

Derivada
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada.

{\displaystyle {d \over dx}e^{x}=e^{x}}Función exponencial compleja
Como en el caso real, la función exponencial puede ser definida como una función holomorfa en el plano complejo de diferentes maneras. Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales.

Comentarios

Publicar un comentario

Entradas populares de este blog

funciones inyectivas, sobreyectivas, biyectivas, identidad y constante.

Imagen
Inyectivas. En matemáticas , una f unción   {\displaystyle f\colon X\to Y}  es  inyectiva  si a elementos distintos del conjunto  {\displaystyle X} ( dominio ) les corresponden elementos distintos en el conjunto  {\displaystyle Y} (condominio)   de  {\displaystyle f} . Es decir, cada elemento del conjunto Y tiene a lo sumo una preimagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen. Así, por ejemplo, la función de números reales  {\displaystyle f:\mathbb {R} \to \mathbb {R} } , dada por  {\displaystyle f(x)=x^{2}}  no es inyectiva, puesto que el valor 4 puede obtenerse como  {\displaystyle f(2)}  Y {\displaystyle f(-2)} . Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  {\displaystyle g:\mathbb {R} ^{+}\to \mathbb {R} ^{+}} , entonces sí se obtiene una función  inyectiva . una función es  inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalment
Leer más

características de cada función representación gráfica

Imagen
FUNCION CONSTANTE Es aquella en la que para cualquier valor de la variable independiente (x), la variable dependiente (f(x)) no cambia, es decir permanece constante. Sea f(x)=c. El dominio de esta función es el conjunto de todos los reales y el recorrido es únicamente el real c   FUNCION LINEAL Es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como: F(x)=mx+b Donde   m y   b son constantes reales y   x es una variable real. La constante m es la pendiente de la recta, y   b es el punto de corte de la recta con el eje   y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica   b, entonces la línea se desplazará hacia arriba o hacia abajo. En el contexto de análisis matemático la función lineal son aquellas con b=0 de la forma: F(x)=mx Mientras que llaman función afín a la que tiene la forma: f(x)
Leer más