funciones inyectivas, sobreyectivas, biyectivas, identidad y constante.

Inyectivas.

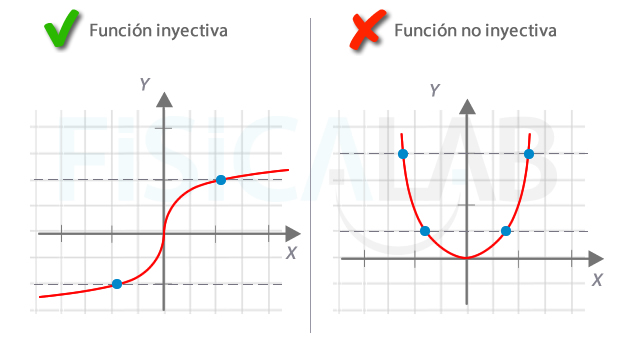
En matemáticas, una función ${\displaystyle f\colon X\to Y}$ es inyectiva si a elementos distintos del conjunto ${\displaystyle X}$(dominio) les corresponden elementos distintos en el conjunto ${\displaystyle Y}$(condominio) de ${\displaystyle f}$. Es decir, cada elemento del conjunto Y tiene a lo sumo una preimagen en X, o, lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.

Así, por ejemplo, la función de números reales ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$, dada por ${\displaystyle f(x)=x^{2}}$ no es inyectiva, puesto que el valor 4 puede obtenerse como ${\displaystyle f(2)}$ Y{\displaystyle f(-2)}. Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función ${\displaystyle g:\mathbb {R} ^{+}\to \mathbb {R} ^{+}}$, entonces sí se obtiene una función inyectiva.

una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:

f

 ∀a,b∈Do

, si f(a)= f(b)⇒a=b

Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.

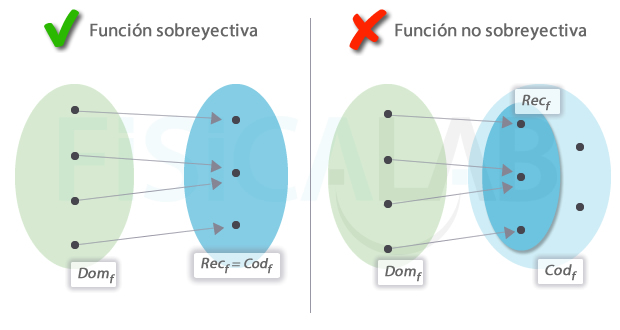
Sobreyectivas.

una función sobreyectiva también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente:

∀y∈Codf ∃x∈Domf / f(x)=y

Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.

Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.

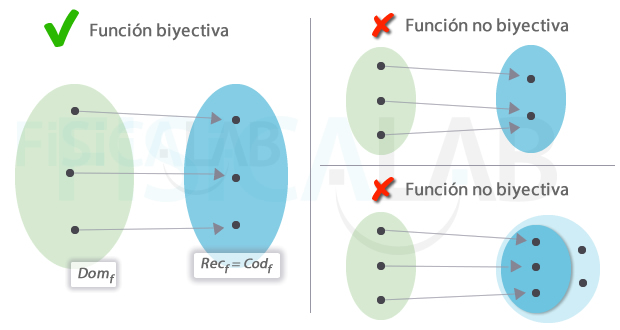
Biyectivas.

Una función es biyectiva cuando es inyectiva y sobreyectiva al mismo tiempo. Formalmente:

∀y∈Codf ∃!x∈Domf / f(x)=y

Es decir, para cualquier elemento y del codominio existe un único elemento x del dominio tal que y es la imagen de x por f.

Identidad.

Una función identidad es una funcion tal que la imagen de cualquier elemento es éste mismo:

La identidad es una función lineal de pendiente m = 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Divide el primer y el tercer cuadrante en partes iguales, o sea, es su bisectriz.

La pendiente es la inclinación con respecto al eje X (eje de abscisas). Al ser ésta positiva (m > 0), la función es creciente.

Que la pendiente de la función identidad sea m = 1 significa que si aumentamos la x en una unidad, la y también aumenta en una unidad.

Formará un ángulo de 45° con cualquiera de los ejes.

La identidad id es el elemento neutro en la composición de funciónes. Es decir, cualquier función f compuesta con la identidad es ella misma.

Constante. 

Una función constante: es una función  tal que la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).

En términos matemáticos, la función es constante si para cualquier par de puntos x₁ y x₂ del dominio tales que x₁<x₂, se cumple que f(x₁) = f(x₂).

La gráfica de una función constante es una recta paralela al eje de abscisas X. También se puede definir una función constante a partir de la derivada. Una función f será constante si para todo punto x del dominio la derivada es nula, es decir f ’(x) = 0. Derivada de la función constante es 0 porque no depende del valor de la variable independiente x.